In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveRoot 2 at {x,y} = { 277, 000} Solve Quadratic Equation by Completing The Square 32 Solving 2x 23x7 = 0 by Completing The Square Divide both sides of the equation by 2 to have 1 as the coefficient of the first term x 2(3/2)x(7/2) = 0 Add 7/2 to both side of the equation x 2(3/2)x = 7/2 Ex 25, 4 Expand each of the following, using suitable identities (x 2y 4z)2 (x 2y 4z)2 Using (a b c)2 = a2 b2 c2 2ab 2bc 2ac Where a = x , b

X 2 3 Expand Novocom Top
Expand 3 x 2 y 7 square
Expand 3 x 2 y 7 square-X 2R ln(1 x) = x x2 2 x3 3 x4 4 x5 5 question is y = ln(1 x) even, odd, or neither?Expand (− 2 x 5 y − 3 z) 2 using suitable identities Hard Answer (− 2 x 5 y − 3 z) 2 is of the form (a b c) 2 (a b c) 2 = a 2 b 2 c 2 2 a b 2 b c 2 c a where a = − 2 x, b = 5 y, c = − 3 z ∴ (− 2 x 5 y − 3 z) 2 = The square of (x x 1




Rules Of Exponents
X y = G What can QuickMath do?Learn about expand using our free math solver with stepbystep solutions(c) h(x)= 1 2x3;
Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graph1 Identify the terms, their coefficients for each of the following expressions In the expression 5xyz 2 – 3zy, the terms are 5xyz 2 and –3zy coefficient of xyz 2 in the term 5xyz 2 is 5 coefficient of zy in the term –3zy is –3 In the expression 1 x x 2, the terms are 1, x and x 2Note y = sinx is an odd function (ie, sin( x) = sin(x)) and the taylor seris of y = sinx has only odd powers = X1 n=1 ( 1)(n 1) x2n 1 (2n 1)!
X3 = ⋯ = 577 408 = And one can quickly check that (x3)2 = , which is pretty much the square root of 2 We want to (manually) approximate √2 by using the first few terms of the binomial series expansion of √1 − 2x = ∞ ∑ n = 0(1 2 n)( − 2x)n x < 1 2 = 1 − x − 1 2x2 − 1 2x3 ⋯ Here we look forExpand polynomial (x3)(x^35x2) GCD of x^42x^39x^246x16 with x^48x^325x^246x16;Harnett, ch 3) A The expected value of a random variable is the arithmetic mean of that variable,



4 The Binomial Theorem




If 3x 5y 9 And 5x 3y 7 Then What Is The Value Of X Y
Expectations Expectations (See also Hays, Appendix B;Quadratic expressions are algebraic expressions where the variable has an exponent of 2 For example x 2 3x 4 To expand quadratic equations, use the FOIL (First, Outside, Inside, Last) method F irst O utside I nside L ast Example One Expand ( x 3 ) ( x 2Remainder of x^32x^25x7 divided by x3;




Graphing Lines Technique 3 Elimination Jx 4y 9 Use Multiplication To Get One Variable X 2y 8 Lx Have X 54 8 Pdf Free Download




X 2 3 Expand Novocom Top
Expand (xy)^2 Rewrite as Expand using the FOIL Method Tap for more steps Apply the distributive property Apply the distributive property Apply the distributive property Simplify and combine like terms Tap for more steps Simplify each term Tap for more steps Multiply by Multiply by Add andQuestion Use The Properties Of Logarithms To Expand The Expression Ln((x Y)^2 Y^3 Z/x^4) Log_7 Squareroot X/4 Use The Properties Of Logarithms To Condense The Expressions To The Logarithm Of A Single Quantity 1/2 Ln(2x 1) 2ln(x 1)The number x is 2 more than the number y If the sum of the squares of x and y is 34, then find the product of x and y In the expansion of (2x 2 8) (x 4) 2;



1




Squaring A Binomial Expii
Expand log of square root of (xy^7)/(z^3) Rewrite as Expand by moving outside the logarithm Rewrite as Expand by moving outside the logarithm Multiply by Rewrite as Expand by moving outside the logarithm Apply the distributive property Simplify Tap for more steps Combine and Multiply Tap for more stepsTaylor series If a function \(f\left( x \right)\) has continuous derivatives up to \(\left( {n 1} \right)\)th order inclusive, then this function can be expanded in Exercise 3 Expand the following expression, writing your answer in its simplest form Be careful of notation and do not use spaces in your answer ( x ) 2 = x 2 x
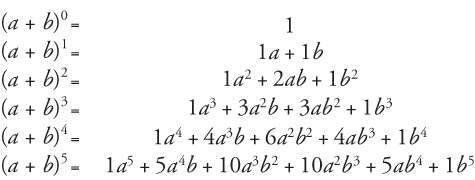



Binomial Coefficients And The Binomial Theorem
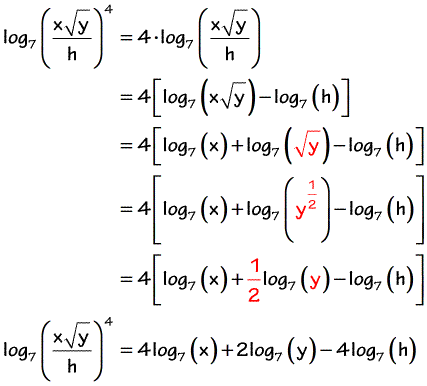



Expanding Logarithms Chilimath
Expand the following product (3 x 1) (2 x 4) `(3x1)(2x4)` returns `3*x*2*x3*x*42*x4` Expand this algebraic expression `(x2)^3` returns `2^33*x*2^23*2*x^2x^3` Note that the result is not returned as the simplest expression in order to be able to follow the steps of calculations To simplify the results, simply use the reduce functionPrecalculus The Binomial Theorem Pascal's Triangle and Binomial Expansion 1 AnswerExpand and Simplify (i) 2(x 4) 3(x 2) (ii) x(x 3) (iii) y(2y 3) (iv) (x 3)(x 4) (v) (x 3)(x 9)




Expand 3 X 4 Y 5 Z Whole Square Brainly In




Expanding Algebraic Expressions Using Identities Worksheets
The perfect cube forms ( x y) 3 (xy)^3 (xy)3 and ( x − y) 3 ( xy)^3 (x −y)3 come up a lot in algebra We will go over how to expand them in the examples below, but you should also take some time to store these forms in memory, since you'll see them often ( x y) 3 = x 3 3 x 2 y 3 x y 2 y 3 ( x − y) 3 = x 3 − 3 x 2 y 3How to expand two brackets algebra How to simplify (x3)(x4)We can use the distributive law for both x and 3 individually and multiply throughSolve Quadratic Equation by Completing The Square 52 Solving x23x10 = 0 by Completing The Square Add 10 to both side of the equation x23x = 10 Now the clever bit Take the coefficient of x , which is 3 , divide by two, giving 3/2 , and finally square it giving 9/4 Add 9/4 to




Expand X 5 X 6 X 7 Novocom Top



The Substitution Method
= 2 x 2 3 x − 10 x − 15 = 2 x 2 − 7 x − 15 1 Expand the brackets by multiplying (2 x 3) by x and (2 x 3) by −5 2 Simplify by collecting like terms 3x − 10x = −7xThe calculator can also make logarithmic expansions of formula of the form ln ( a b) by giving the results in exact form thus to expand ln ( x 3), enter expand_log ( ln ( x 3)) , after calculation, the result is returned The calculator makes it possible to obtain the logarithmic expansionQuotient of x^38x^217x6 with x3;




Expanding Algebraic Expressions Using Identities Worksheets



Squaring Binomials
Take the square root of both sides of the equation x^ {2}y^ {2}3=0 Subtract 3 from both sides y^ {2}x^ {2}3=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0Sinx = x x3 3!SOLUTION 15 Since the equation x 2 xy y 2 = 3 represents an ellipse, the largest and smallest values of y will occur at the highest and lowest points of the ellipse This is where tangent lines to the graph are horizontal, ie, where the first derivative y'=0




The Binomial Theorem Explained With A Special Splash Of Pascal S By Brett Berry Math Hacks Medium



Expand X Y 7 X 2 6 A 2 2b 5 Find The Chegg Com
Expand (x 2 3) 6; Anyway, I mean the row that starts 1, 7 Each number is formed by adding the two numbers above to the left and right The last row gives us the coefficients we need (xy)^7 = x^77x^6y21x^5y^235x^4y^335x^3y^421x^2y^57xy^6y^7Click here👆to get an answer to your question ️ Expand (2x 3y)^2
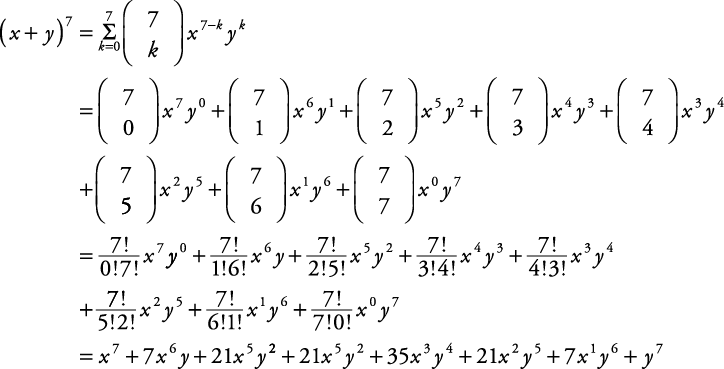



Binomial Coefficients And The Binomial Theorem




3 3 Determinants By Expansion Wolfram Demonstrations Project
I sure don't, because the zero power on the outside means thatFind the value of (i) coefficient of x 3 (ii) coefficient of x 2 find the sum of their square Solution 12 Let a, b be the two numbers 'Checklist Ready to be marked ?
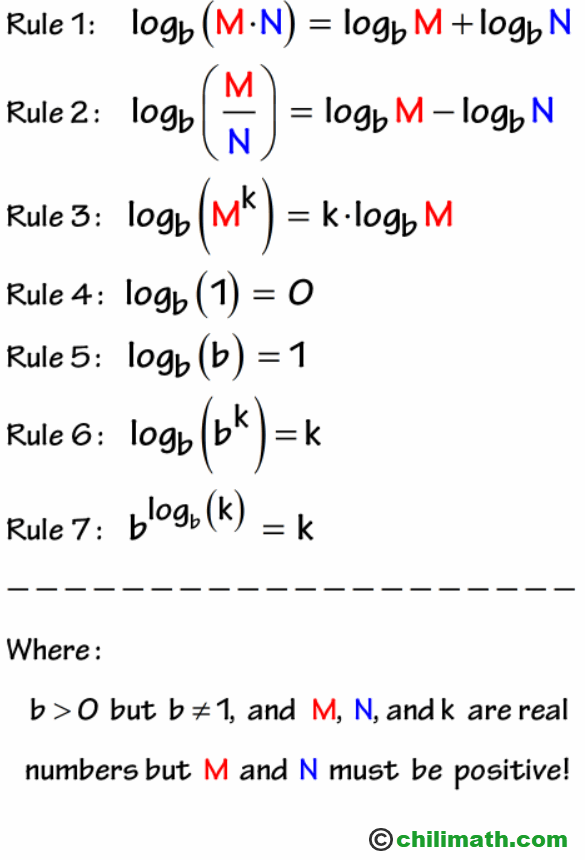



Expanding Logarithms Chilimath




Maclaurin Expansion For 1 Sqrt X 2 9 Mathematics Stack Exchange
Expand (i) (3x – 4y 5z)2 (ii) (2a – 5b – 4c)2 (iii) (5x 3y)3 (iv) (6a – 7b)3Or= X1 n=0 ( 1)n x2n1 (2n 1)!In that case −3 5 = 15 (a positive answer), but here is an example where the second part is negative So the second term ended up negative because 2x −a = −2ax, (it is also neater to write "−2ax" rather than "−2xa") That was also interesting because of x being squared (x 2) Lastly, we have an example with three terms inside




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube




Unit 2 Algebra Mathematics 9 1 Igcse Year Ppt Download
Students trying to do this expansion in their heads tend to mess up the powers But this isn't the time to worry about that square on the xI need to start my answer by plugging the terms and power into the TheoremThe first term in the binomial is "x 2", the second term in "3", and the power n is 6, so, counting from 0 to 6, the Binomial Theorem gives me= X1 n=1 ( 1)(n 1) xn n =or X1 nA =1 Solution (a) We shall use (1) by &rst rewriting the function as follows 1 1x2 1 1¡(¡x2) y==¡x2 1 1¡y = X1 n=0 yn;




3 Binomial Theorem Example 1 A Basic Binomial Expansion Question To Get Used To The Formula Youtube




Pls Solve It Fast 5 6 8 9 14 15 Expand Use Appropriate Formulae Maths Meritnation Com
China this week revealed plans to drastically expand an experimental weather modification program to cover an area of over 55 million square kilometers (21 million square miles) more than 15Solve 1 √2x 3 = 6 Show Solution Begin by subtracting 1 from both sides in order to isolate the radical term Then square both sides to remove the binomial from the radical 1 √ 2 x 3 − 1 = 6 − 1 √ 2 x 3 = 5 ( √ 2 x 3) 2 = ( 5) 2 Simplify the equation and solve for x 2 x 3 = 25 2 x = 22 x Question 5 Find the remainder when x 3 x 2 x 1 is divided by x – using remainder theorem Solution Let p (x) = x 3 x 2 x 1 and q (x) = x – Here, p (x) is divided by q (x) ∴ By using remainder theorem, we have Question 6 Find the common factor in the quadratic polynomials x 2 8x 15 and x 2 3x – 10



Q Tbn And9gctcrjiceibqwhzu3vqdgtw2xxyia3kyngh1xmyz7k3wvplis3fo Usqp Cau




Misc 2 Find A If Coefficients Of X2 X3 In 3 Ax 9 Are Equal
(21 x 5) / (3 x 4) = (21 / 3)(x 5 / x 4) Simplify = 7 x (6 x 4)(4 y 2) / (3 x 2)(16 y) Multiply terms in numerator and denominator and simplify (6 x 4)(4 y 2) / (3 x 2)(16 y) = (24 x 4 y 2) / (48 x 2 y) Rewrite as follows = (24 / 48)(x 4 / x 2)(y 2 / y) Simplify = (1 / 2) x 2 yView more examples » Access instant learning tools Get immediate feedback and guidance with stepbystep solutions and WolframFor jyj < 1 Formula (1) leads to
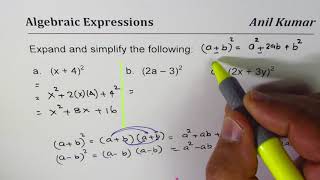



Expand And Simplify Binomial Squares 2x 3y 2 Youtube




7 Ways To Factor Second Degree Polynomials Quadratic Equations
T e In mathematics, the Taylor series of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point For most common functions, the function and the sum of its Taylor series are equal near this pointQuickMath will automatically answer the most common problems in algebra, equations and calculus faced by highschool and college students The algebra section allows you to expand, factor or simplify virtually any expression you choose It also has commands for splitting fractions into partial fractionsLogxy logxlogy = Use property 3 to rewrite the multiplication as addition 3 3 = 2logx7logy Use Property 5 to move the exponents out front Thus, ( ) 27 3 3 3 logxy 2logx7logy = Example 2 Use the properties of logarithms to expand 8 3 x log y æ ö ç ÷ ç ÷ Ł ł 1 2 8 8 3 3 x x log log y y æ ö



1




Simplifying Square Root Expressions Video Khan Academy
The distributive property is the rule that relates addition and multiplication Specifically, it states that a ( b c) = a b a c a (bc) = ab ac a(bc) = abac ( a b) c = a c b c (ab)c = ac bc (ab)c = acbc It is a useful tool for expanding expressions,Simplify (3x 4 y 7 z 12) 5 (–5x 9 y 3 z 4) 2 0 Who cares about that stuff inside the square brackets?3) Simplify left side FOIL or use extended distribution on the right side to eliminate the exponents x 15 = 225 30√ (x) x 4) Subtract x 15 = 225 30√ (x) 5) Subtract 225 210 = 30√ (x) 6) Divide by 30 7 = √ (x) 7) Square both sides again 7^2 = √ (x)^2 8) Simplify 49 = x




Expand 3x 7y Z 2 Using Identities Brainly In




Expand 3 X 4 Y 5 Z Whole Square Brainly In
This calculator can be used to expand and simplify any polynomial expression How do you expand the binomial #(x2)^3#?(b) g(x)= x x2;



2




X 2 3 Expand Novocom Top
The following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) CubeAlgebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank you




Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11




Polynomial Functions




Find Middle Term For Even Power Binimial Expansion Youtube




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu




Binomial Theorem Wikipedia




Use Identity And Expand 3x 2y 7 2 Brainly In




Polynomial Functions
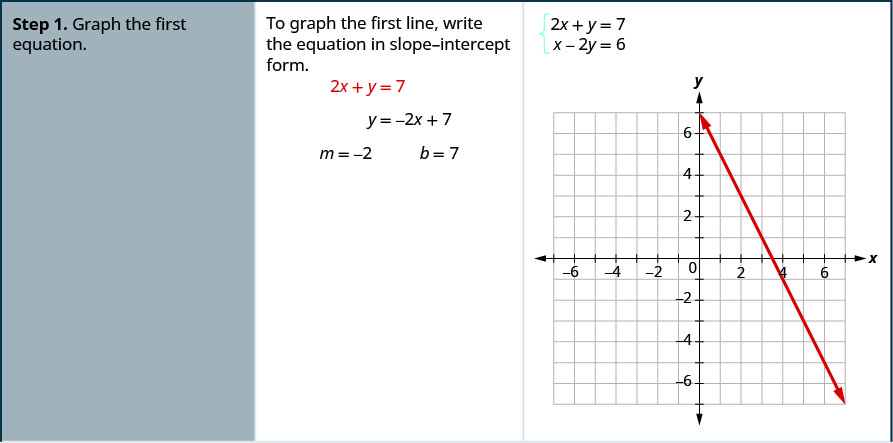



4 1 Solve Systems Of Linear Equations With Two Variables Mathematics Libretexts



Solve Quadratic Equations Using The Quadratic Formula Elementary Algebra



2




Ex 2 5 4 Expand Each Of The Following Using Suitable




Simplify Simplify Radical Rational Expression With Step By Step Math Problem Solver




Partial Fractions Calculator Wolfram Alpha
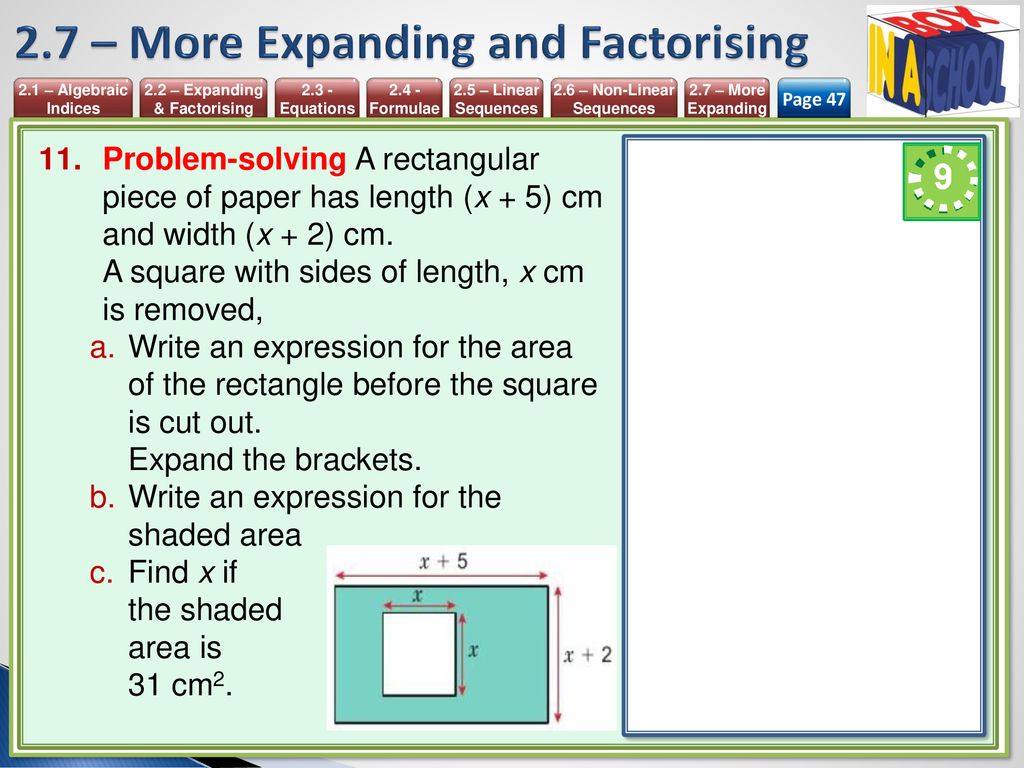



Unit 2 Algebra Mathematics 9 1 Igcse Year Ppt Download




Powers In Brackets How To Use The Bracket Power Rule Owlcation




Intro To The Binomial Theorem Video Khan Academy




Mathematics Ii Tranquileducation




Solved 1 Find The Constant Term In The Expansion Of 1 7 Chegg Com




Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu
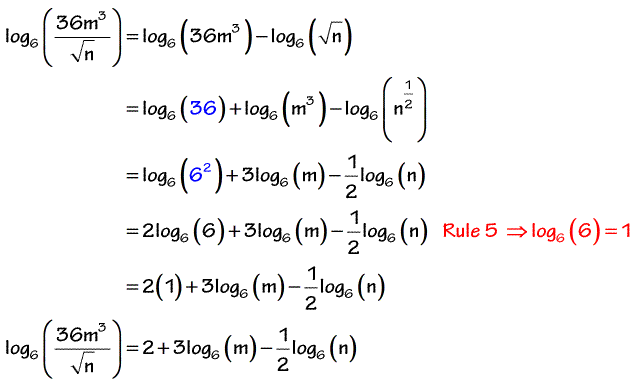



Expanding Logarithms Chilimath




Rules Of Exponents



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Cube Algebra Wikipedia




Factor Factor A Polynomial And Trinomial With Step By Step Math Problem Solver



What Is The Binomial Expansion Of Math 1 X 2 Math Quora




Rules Of Exponents




Expanding Simplifying Algebraic Expressions Video Lesson Transcript Study Com




Expanded Notation Video Lessons Examples Solutions




Forming Polynomial Equations With Roots Video Lesson Transcript Study Com



2




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Monday Announcements Progress Reports This Thursday 3 Rd Period Tuesday Wednesday Starr Testing So No Tutorials 30 Minute Classes Tuesday Periods 1 3 5 7 Ppt Download




Implify The Expression S R 1 2 8r 7 A R 11 B Chegg Com



2




Simplifying Expanding And Factoring Expressions Tpt




Expand Each Of The Following Using Suitable Identities I X 2y 4z 2 Ii 2x Y Z Youtube
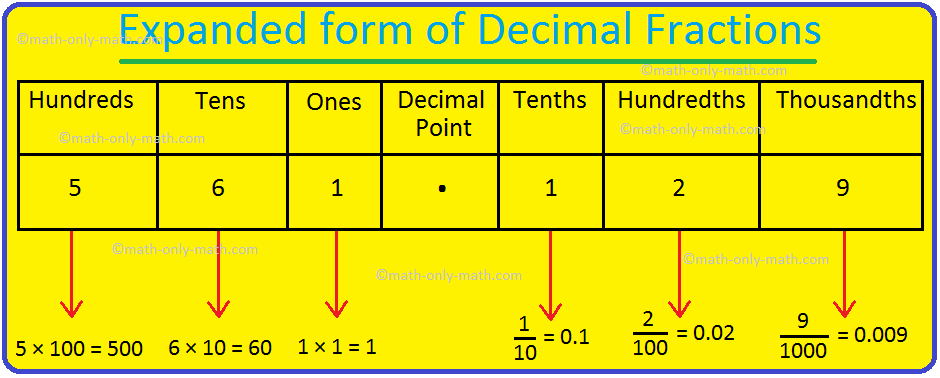



Expanded Form Of Decimal Fractions How To Write A Decimal In Expanded




Binomial Theorem Wikipedia




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9




Exponent Rules 7 Key Strategies To Solve Tough Equations Prodigy Education




How To Find The Degree Of A Polynomial 14 Steps With Pictures




Binomial Theorem Finding The Coefficient Of X 3 In 2 4x 5 Youtube



11 Factor Then Expand The Logarithm The First Blank Chegg Com
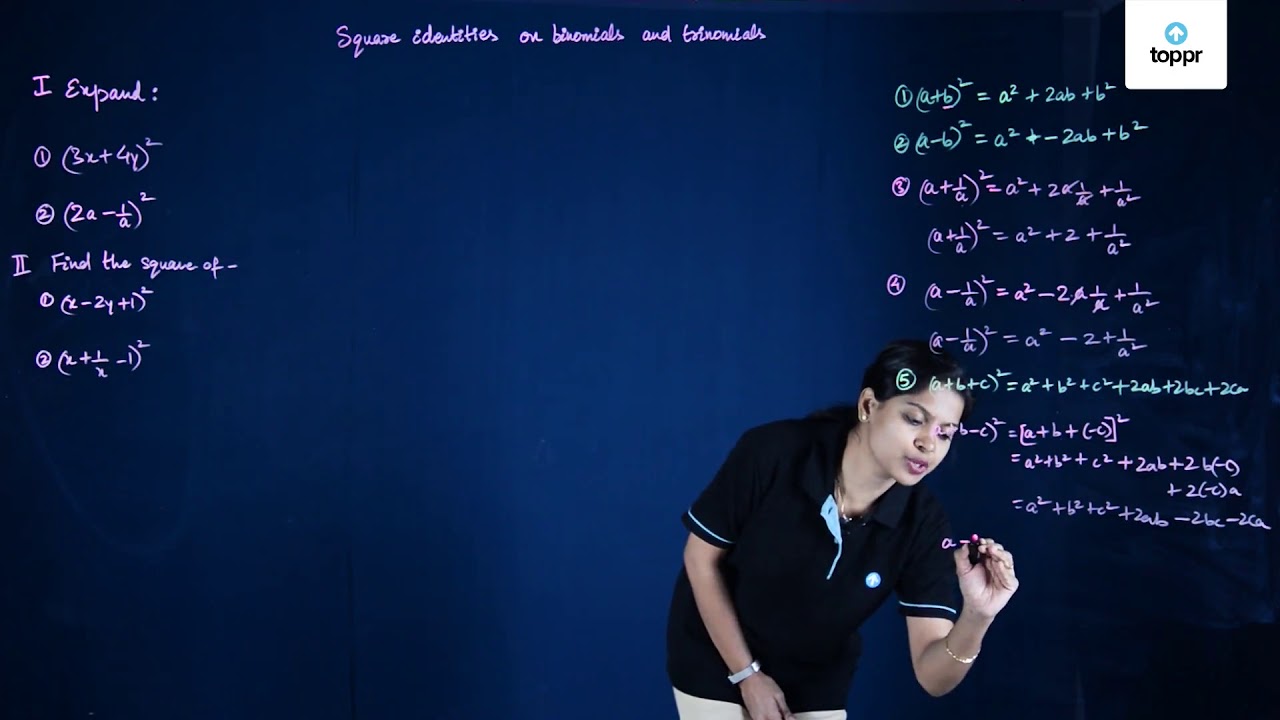



Monomial Binomial Trinomial And Polynomials Videos And Examples



The Substitution Method




Pdf G3z3002 Minitest Bash Bash Academia Edu




Perfect Square Factorization Intro Video Khan Academy



2




The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets



4 The Binomial Theorem



2



2




Graph Graph Inequalities With Step By Step Math Problem Solver




Expand And Simplify Gcse Maths Lesson Examples Worksheet



2
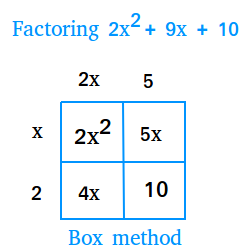



Factoring Using The Box Method




X 2 3 Expand Novocom Top




Simplify Simplify Radical Rational Expression With Step By Step Math Problem Solver
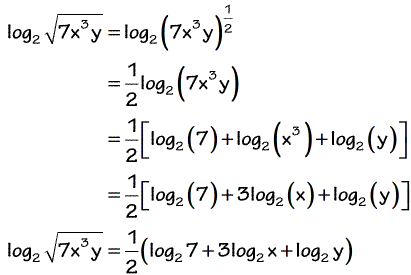



Expanding Logarithms Chilimath



Q 85 Using A Suitable Identity Expand The Following 3x 2y 7 2 Brainly In



Expand The Following 3x 2y 7 Sq Brainly In




Write The Following In Expanded Form X 2y 3z 2 Ii X



What Is The Binomial Expansion Of Math 1 X 2 Math Quora




Use Properties Of Logarithms To Expand Each Logarithm Chegg Com



1



Square Root Of 2 Wikipedia




Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9



How To Solve For X And Y In X Y 5 And Xy 6 Quora




Example 10 Find Term Independent Of X In 3 2 X 2 1 3x 6
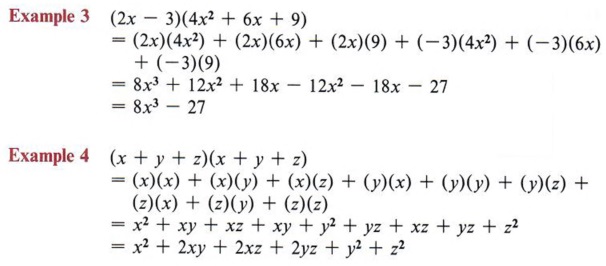



Expand Expand Terms Multiply Polynomials With Step By Step Math Problem Solver



0 件のコメント:
コメントを投稿